CCGraph：a PDG-based code clone detector with approximate graph matching

CCGraph

论文题目：(2020-ASE) CCGraph：a PDG-based code clone detector with approximate graph matching ——具有近似图匹配的基于PDG的代码克隆检测器

论文引用：Zou Y, Ban B, Xue Y, et al. CCGraph: a PDG-based code clone detector with approximate graph matching[C]//2020 35th IEEE/ACM International Conference on Automated Software Engineering (ASE). IEEE, 2020: 931-942.

一、主要内容

本文提出了一种新颖的基于程序依赖图（program dependency graph，PDG）的代码克隆检测器CCGraph，它使用图形内核。PDG的结构进行规范化，并通过测量代码的特征向量来设计两阶段过滤策略。使用一种基于重整WL（Reforming Weisfeiler-Lehman）图内核的近似图匹配算法来检测代码克隆。

二、背景介绍

研究现状

在实际软件项目中，代码克隆是指复制粘贴式的代码复用或者模式化思维所造成的相同或相似代码重复出现的现象。

由于开发风格因人而异，对同一功能的不同实现方式导致文本差异较大的高级别克隆在软件中广泛存在，不利于后续开发人员对代码的解读和维护，也增加了对软件进行二次开发的难度。

  • 因此，高级别代码克隆的检测可以帮助程序开发人员定位这些克隆代码，然后进行代码重构和系统维护，在软件开发过程中十分重要。

目前在学术界，相关研究者按照源码文本之间的相似程度将代码克隆划分为４个级别

  1. Type-1 的代码克隆是指除了空白、注释和布局之外完全相同的代码。
  2. Type-2 的代码克隆是指在 Type-1的基础上，除了标识名、变量名、变量类型和函数名以外完全相同的代码。
  3. Type-3 的代码克隆是指在Type-2的基础上存在着一定的插入、删除和修改语句的相似的代码。
  4. Type-4 的代码克隆是指功能相似但是通过不同的语法方式实现的代码。
  5. 对于 Type-3 和 Type-4 的高级别代码克隆检测，目前已经有一些国内外的学者进行了相关研究，其中基于程序依赖图 PDG (Program Dependency Graph)的方法是一类重要的检测方法。

现有的基于PDG的代码克隆检测方法首先使用静态分析工具来构建包含源码语法结构及调用关系、数据流等的程序依赖图，再采用子图同构检测等精确图匹配算法找出2个相同或相似的PDG，以此发现克隆代码。

  • 但是，子图同构检测算法是经典的NP难问题，算法的高复杂度会导致时间消耗巨大，无法用于检测大型的软件系统，而且这种精确的图匹配算法容错率低，也会导致克隆代码的检出率低。

本文提出了一种基于 Weisfeiler-Lehman 图核算法的代码克隆检测方法。

  • 本方法首先对PDG的结构进行了简化；
  • 然后使用特征向量相似度的计算进行候选代码对的过滤；
  • 最后采用 Weisfeiler-Lehman图核这种非精确图匹配的算法进行PDG的相似度计算。

能够更高效地检测出更多的高级别克隆。

图匹配算法

图匹配算法可分为精确匹配和非精确匹配算法。精确图匹配算法主要是通过子图同构匹配来判断图相似度，精确图匹配大都是 NP 难问题，检测算法时间消耗过大，且还会降低对图结构误差的容忍性。

非精确图匹配算法主要是通过将图结构识别转为统计识别问题，找到精确图匹配最好的近似解，主要包括图嵌入和图核 2 种算法。图嵌入是指提取图的一些特征值进行相似度比较。这种降维处理损失了图中包含的大量结构信息，会降低图匹配精度，可以用于过滤操作。图核算法是把图映射到向量特征空间，使得2 个图的相似性等于它们在向量特征空间中的内积。

图核算法具体的流程如下所示：

  1. 给定 2 个图 G1(V1,E1)G_{1}(V_1,E_1)、G2(V2,E2)G_{2}(V_2,E_2)、以及一种图分解方式 F，分解后的子结构为：

F(G1)=S1,1,S1,2...S1,N1F(G2)=S2,1,S2,2...S2,N2F(G_1)= {S_{1,1},S_{1,2}...S_{1,N_1}} \\ F(G_2)= {S_{2,1},S_{2,2}...S_{2,N_2}}

  1. 基于上述子结构， G1G_1、G2G_2 的图核值可以表示为：

kR(G1,G2)=∑n1=1N1∑n2=1N2σ(S1,n1,S2,n2)k_{R}(G_1,G_2)=\sum_{n_1=1}^{N_1}\sum_{n_2=1}^{N_2}\sigma(S_{1,n_1},S_{2,n_2})

其中，σ(S1,n1,S2,n2)\sigma(S_{1,n_1},S_{2,n_2})在 S1,n1S_{1,n_1} 和 S2,n2S_{2,n_2} 同构时为1，不同构时为0。因此，任何一种图分解方式和子结构同构判断方式的组合都可以定义出一个新的图核。这种算法既保留了核函数计算效率高的优点，也包含了图数据的结构化信息

三、设计实现

本文首先生成了源代码中函数级别的程序依赖图，并对生成的图结构设计了约简的策略，随后对候选的代码对集合进行特征向量的提取和过滤，最后应用Weisfeiler-Lehman图核算法进行图相似性的比较，找出代码克隆；其总体流程图如图：

image-20210319165740835

PDG 的生成和简化

本文选取TinyPDG工具进行改进，用于PDG的生成。TinyPDG将源代码程序生成对应的PDG后通过 dot 文件类型存储。

  • 通过节点编号、形状等属性来表示语句的不同类型，例如声明语句、控制语句和赋值语句
  • 通过边的形状来表示语句间的控制依赖、数据依赖以及地址依赖关系。
  • 然后对PDG按照函数级别进行了切分，剔除了工具自动生成的与语法无关的节点，例如函数进入和退出节点。
  • 最后对函数中一些冗余子图进行了合并，例如第三方函数调用子图，这样可以缩小PDG的规模，从而减少后续图匹配算法的时间消耗

image-20210319171030445

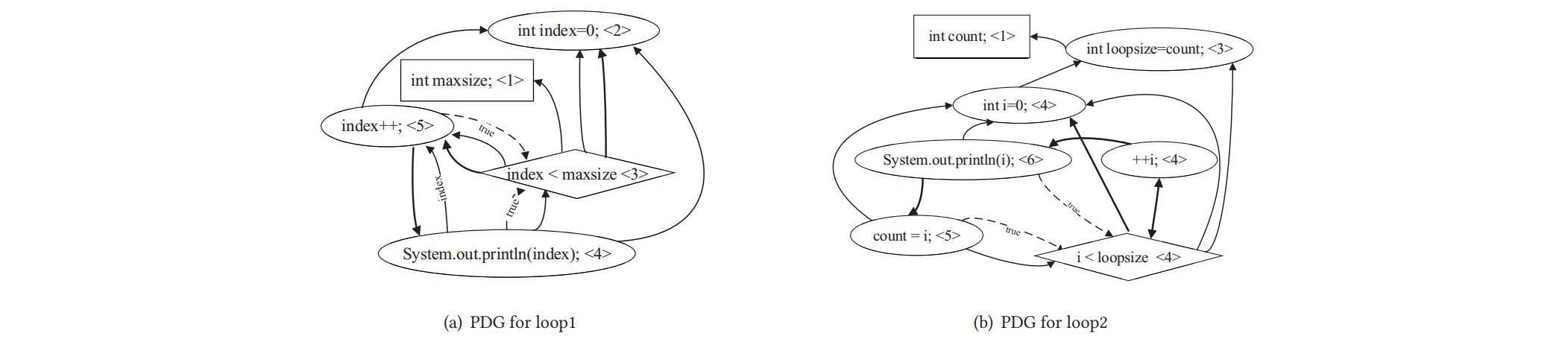
image-20210319171042492

代码程序依赖图示例

PDG 集合的过滤

针对候选的代码对集合，本文首先进行规模比过滤：

  1. 如果 2 个图的节点数相差过大，则过滤掉该候选对。然后统计了PDG中不同依赖关系的边的条数和不同类型的节点数目组成特征向量
  2. 进行余弦相似度的计算，小于给定阈值的候选对会被直接过滤掉。这样可以大大缩小后续需要进行图匹配的PDG 对规模，提升速度。

基于 Weisfeiler-Lehman 核的克隆检测

克隆检测方法流程

针对程序依赖图的结构特征，本文使用并改进Weisfeiler-Lehman图核算法来进行有向有标签图的相似度匹配。Weisfeiler-Lehman图核算法的基本思想是：对每个节点的所有邻接节点的集合的标签进行排序，然后把这些标签根据某一映射压缩成新的更短的标签值：

  1. 给定 G1 和 G2，网络中每个节点有一个label，如图中的1，2，3，4，5
  2. 标签初始化并且将多重集合标签排序，做一阶广度优先搜索，即只遍历自己的邻居。
    • 比如在图(a) 网络G中原(5)号节点，变成(5,234)，这是因为原节点的一阶邻居有2、3和4
  3. 标签压缩：仅仅只是把扩展标签映射成一个新标签，如 5,234 = >13
  4. 压缩标签替换扩展标签
  5. 顶点标签重新赋值；

image-20210319171237969

Weisfeiler-Lehman图核一次迭代过程

假设要测试同构的两张图为G 和 G’，那么在结点u的第 i 次迭代里，算法都分别做了四步处理：标签复合集定义、复合集排序、标签压缩和重标签。

  • 事实上，Weisfeiler-Lehman算法在大多数图上会得到一个独一无二的特征集合，这意味着图上的每一个节点都有着独一无二的角色定位。
  • 对于大多数非规则的图结构，得到的特征可以作为图是否同构的判别依据

当要判断Graph1和Graph2是否同构时，WL test的主要步骤如下图所示，通过聚合节点邻居的label，然后通过 hash 函数得到节点新的label，不断重复直到每个节点的label稳定不变：

img

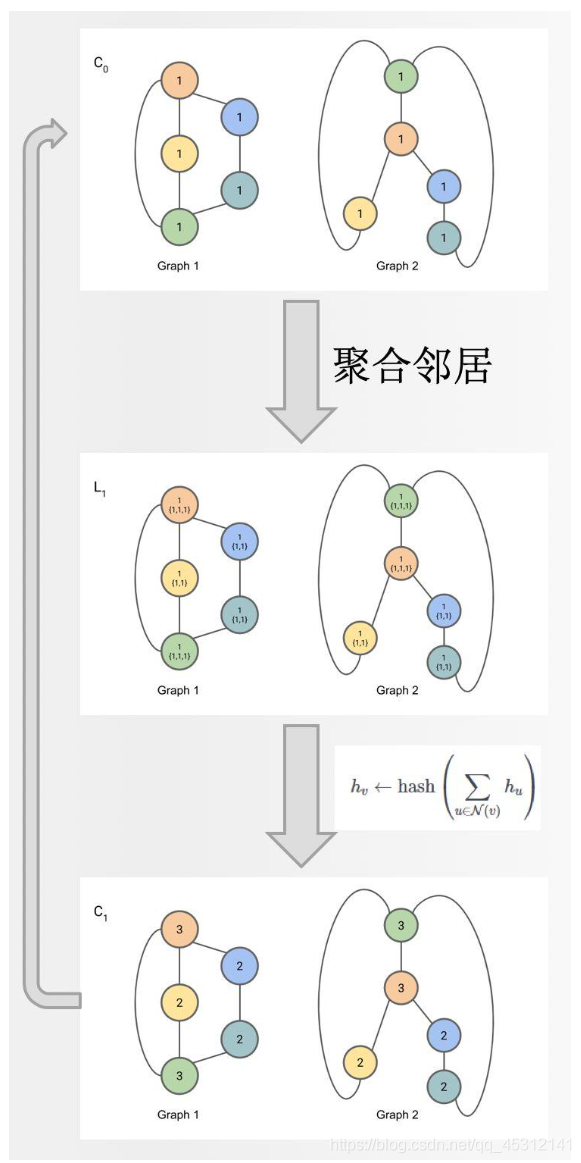
稳定后，统计两张图的 label的分布，如果分布相同，则一般认为两张图时同构的。

稳定时：统计各个label的分布

  • 图1：1个8，2个7，2个9
  • 图2：1个8，2个7，2个9

则，我们不排除其同构的可能性

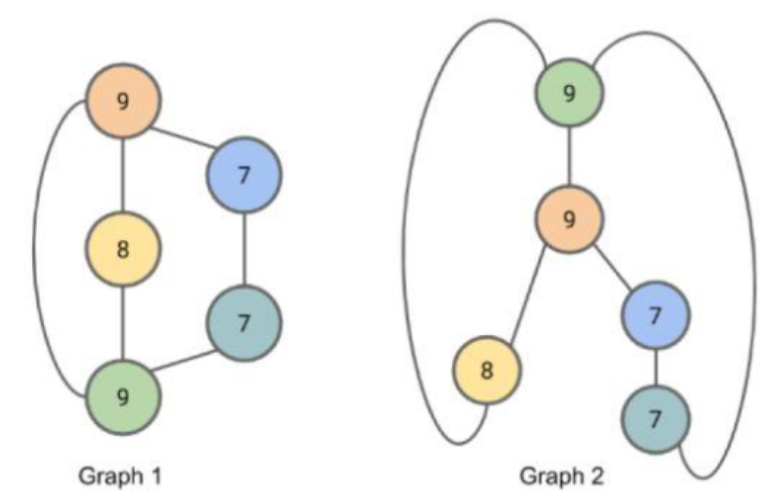
image-20210321090706170

Weisfeiler-Lehman图核方法的步骤和GNNs具有异曲同工之妙，都是通过不断聚合邻居信息，得到节点的新表示。

因此，基于Weisfeiler-Lehman图核的图匹配算法及改进步骤如下所示：

  1. 对PDG图中每个节点的标签按照语法类别进行 Hash 处理，将其结果作为图的初始标记。
  2. 在设定的 h 次迭代过程中，每次迭代都将当前节点的邻居节点的标签汇集在当前节点中，再对该标签序列使用局部敏感哈希算法进行压缩更新，得到新的节点标签。
  3. 迭代过程完成后，若更新后 2个节点的标签相同，则认为以这2个节点为根节点，高度为 h 的子树存在同构。
  4. 计算出 2 个图结构间节点标签集合中相同的节点标签对数，即为图核的值；若2个图的图核值满足设定的阈值范围，则认为 2 段代码为克隆代码。
  5. 动态设定迭代次数，每次迭代完成后统计图中相同标签的节点数目。
  6. 在第 n 次迭代过程加入权重因子，对低次的迭代赋予更高的权重

在基于 Weisfeiler-Lehman 图核算法的图匹配之后，即可计算代码对的图核值，代表着 2 个图中相似点的总数量。本文使用图核值与较小的程序依赖图的比例作为 2 个图的相似度，如果相似度大于设定的阈值，则认为该代码对为代码克隆。

四、实验评估

实验环境

实验平台

单机 Ubuntu14.04 LTS 四核 8GB 内存的操作系统下进行。

实验数据

在CCGraph 上针对C代码的CCSharp 和Java代码的Oreo在几个代码数据集上进行了实验。

由于PDG生成只能应用于可编译代码，因此选择了一些高质量的真实世界代码数据集，并通过各种伪装从真实世界代码中开发了一些人工代码数据集

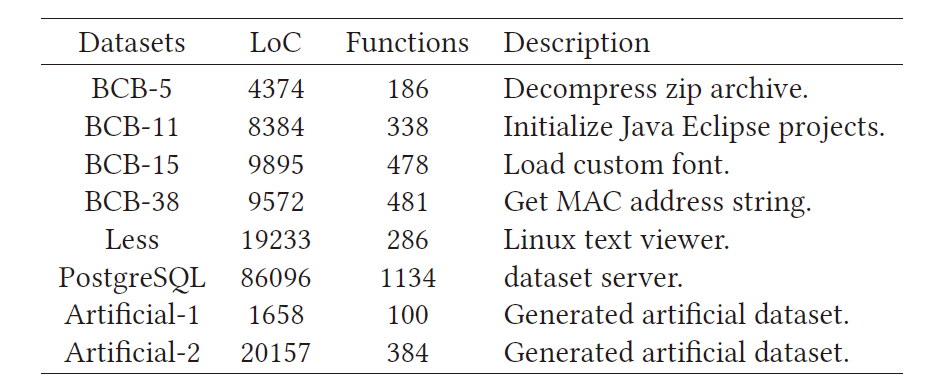
image-20210321104234483

评估标准

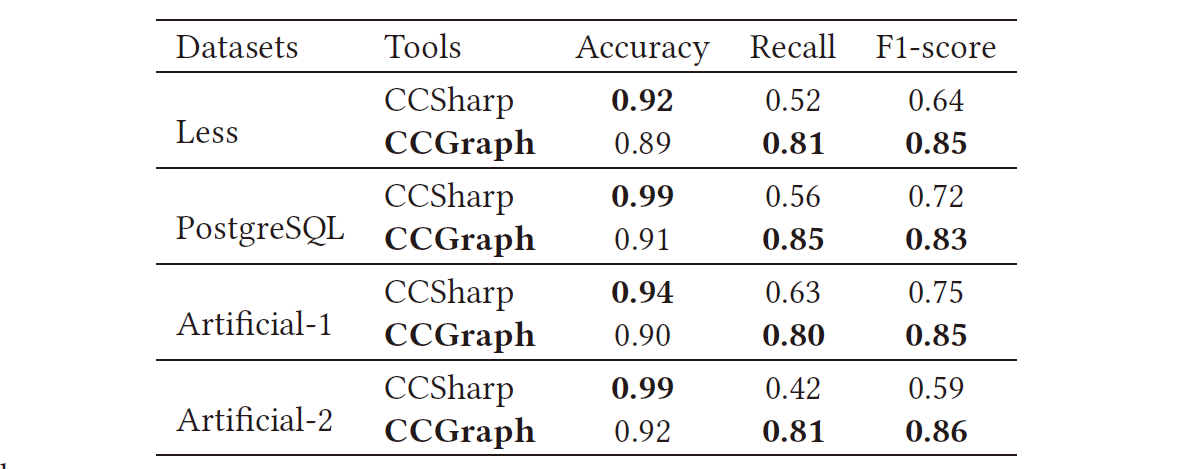
代码集合中检测出克隆代码对的精确率、召回率和时间性能3个评估标准：

对比方法

  1. 基于token的检测方法：CCAligner、 SourcererCC、NICAD
  2. 基于AST的方法 DECKARD
  3. 由于基于PDG的克隆检测方法 Oreo 工具进行对比实验

PDG 结构简化的效率

测试PDG结构简化对几个典型数据集的影响。这些策略有效地简化了PDG，并且不破坏原始语义信息，效率结果如表3所示。因为图匹配带来的时间成本随着节点和边的数量的增加而呈指数增长。通过删除无意义的节点并合并功能调用子PDG来减小PDG的大小，对于以下克隆检测过程非常有益。

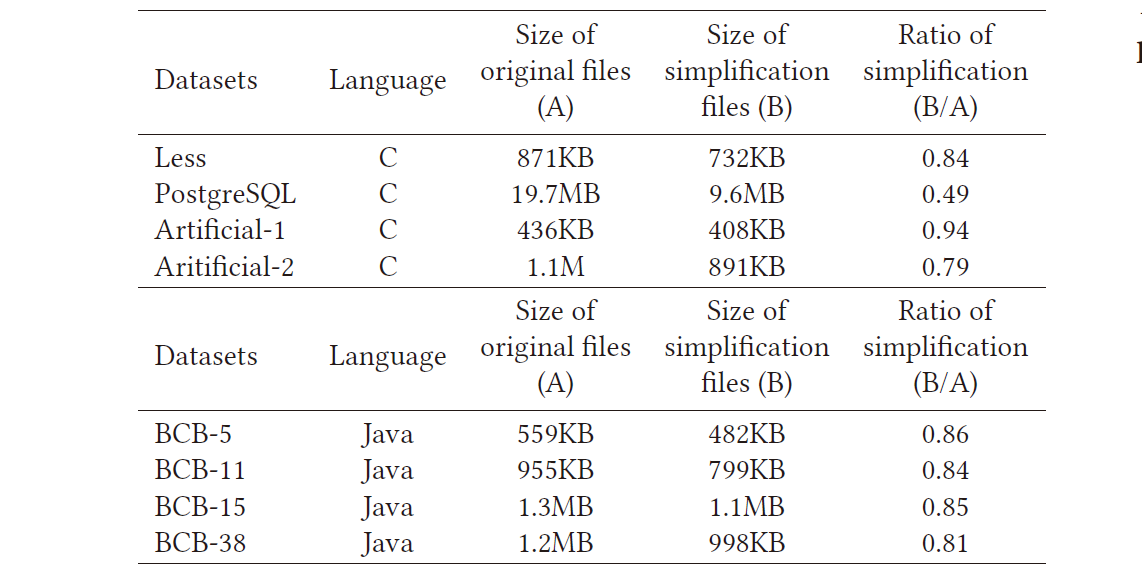
image-20210321104403547

Efficiency of PDG Structure Simplification

过滤策略的效率

实施了启发式过滤策略，过滤效率的结果显示在表4中。

Efficiency of Filtering Strategies on Datasets

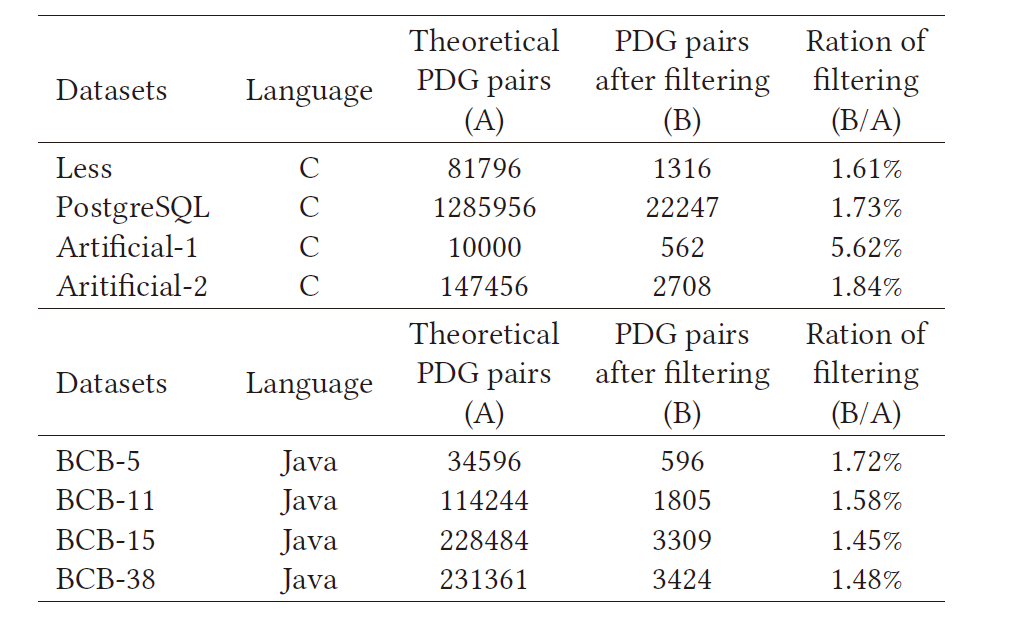
image-20210321104516144

过滤率是指过滤后的PDG对的数量除以总PDG对的数量。它可以排除大多数候选PDG对，并有助于稍后加速图形匹配过程。

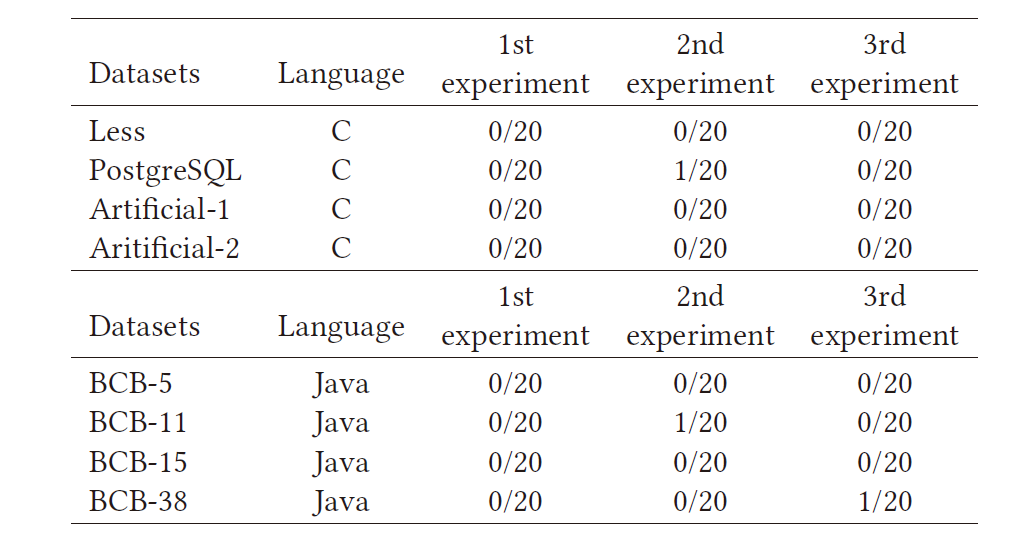
  1. 从每个数据集的过滤后的PDG对中随机选择了20个PDG对，进行了三次，并确定了在20个PDG对中被误过滤的克隆对的数量。
  2. 根据表5所示的结果，我们过滤错误的克隆对的数量非常少，这也验证了过滤策略的有效性.

The Number of Misfiltered Clone Pairs of 3 Sampling Examinations

image-20210321104542299

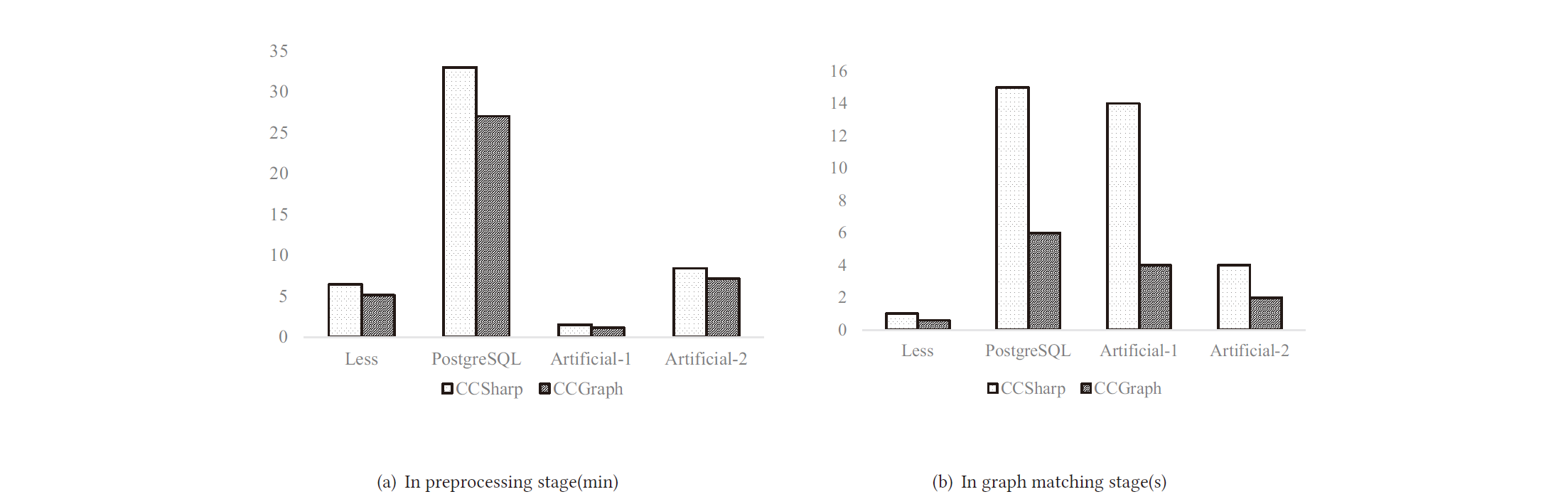
image-20210321104633498

Time cost comparison between CCSharp and CCGraph

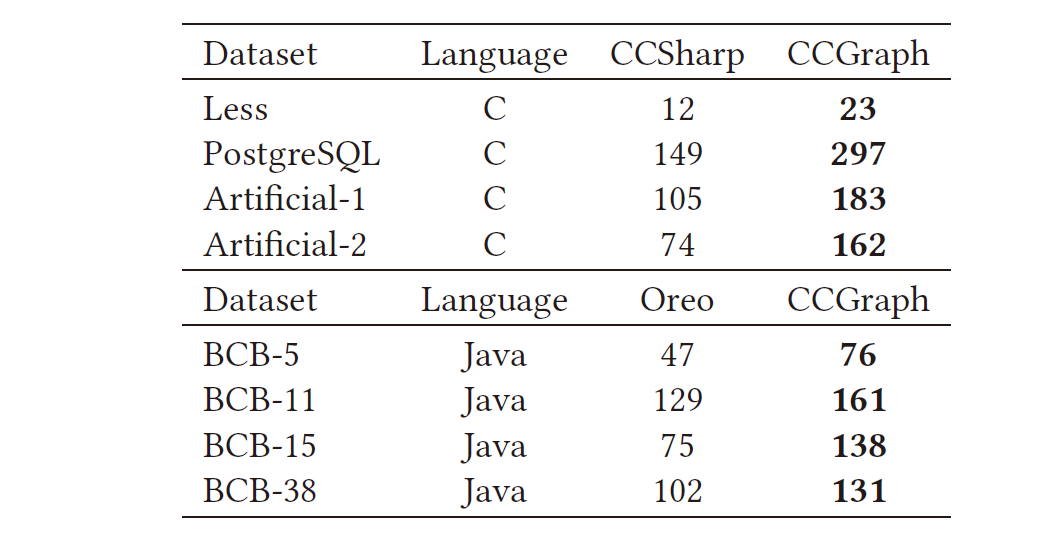
image-20210321104652563

CCGraph针对其他工具检测到的克隆数

image-20210321104707019